esercizio Risolvere la disequazione sen x - cos x < 0 stavolta l'equazione associata e' di tipo gia' visto: per risolverla come equazione basterebbe dividere tutti i termini per cos x essendo una disequazione non posso dividere immediatamente per cos x perche' non ne conosco il segno (ti ricordo che moltiplicando una disequazione per un termine negativo il verso cambia) Allora per risolvere la disequazione distinguiamo due casi cos x > 0 in questo caso, dividendo per cos x, il verso della disequazione resta lo stesso cos x < 0 in questo caso, dividendo per cos x, cambieremo il verso alla disequazione primo caso cos x > 0 sen x cos x 0 ---------- - ---------- < ---------- cos x cos x cos x siccome senx/cosx = tangx cos x > 0 tang x - 1 < 0 Attenzione! 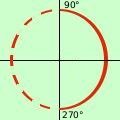Stavolta e' un sistema e dobbiamo cercare solo le soluzioni valide e anche se cercando i segni discordi otterremmo lo stesso risultato (di entrambe i casi) e' concettualmente sbagliato il considerarlo cos x > 0 so che il coseno e' positivo tra 0° e 90° ed anche tra 270° e 360°, quindi 0° < x < 90° U 270° < x < 360° con U indico l'unione degli intervalli a destra la rappresentazione grafica; il punto 0° = 360° e' escluso tang x - 1 < 0 tang x < 1 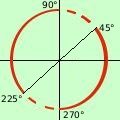so che la tangente e' minore di 1 se l' angolo e' compreso fra 0° 45° ed anche tra 90° e 180° inoltre (essendo la tangente periodica di 180° fra 180° e 225° e tra 270° e 360°; quindi posso scrivere 0° < x < 45° U 90° < x < 225° U 270° < x < 360° a destra la rappresentazione grafica 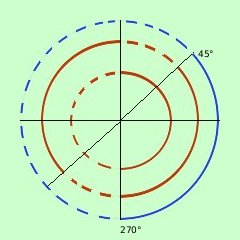mettiamo assieme le soluzioni e risolviamo il sistema 0°<x <90° U 270°<x<360° 0°<x <45° U 90°<x<225° U 270°<x<360° a destra la rappresentazione grafica Soluzione prima parte 0° < x < 45° U 270° < x < 360° secondo caso cos x < 0 sen x cos x 0 ---------- - ---------- > ---------- cos x cos x cos x siccome senx/cosx = tangx cos x < 0 tang x - 1 > 0 Anche qui e' un sistema e dobbiamo cercare solo le soluzioni valide e anche se cercando i segni discordi otterremmo lo stesso risultato (di entrambe i casi) e' concettualmente sbagliato il considerarlo 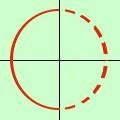cos x < 0 so che il coseno e' negativo tra 90° e 270° quindi 90° < x < 270° a destra la rappresentazione grafica; tang x - 1 > 0 tang x > 1 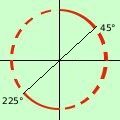so che la tangente e' maggiore di 1 se l' angolo e' compreso fra 45° e 90° e inoltre (essendo la tangente periodica di 180° fra 225° e 270°; quindi posso scrivere 45° < x < 90° U 225° < x < 270° a destra la rappresentazione grafica 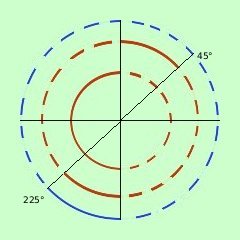mettiamo assieme le soluzioni e risolviamo il sistema 90° < x < 270° 45° < x < 90° U 225° < x < 270° a destra la rappresentazione grafica Soluzione seconda parte 225° < x < 270° Ora devo prendere sia le soluzioni del primo che del secondo sistema: quindi 0° < x < 45° U 225° < x < 270° U 270° < x < 360° il valore 270° e' escluso perche' li' il coseno vale zero e quindi non posso unire gli intervalli